Боковое ребро правильной пирамиды, формула
 |
Боковое ребро правильной пирамиды находится по формуле
\[ b = \sqrt{ h^2 + \Big( \frac{a}{2\sin(\frac{180°}{n})} \Big) ^2 } \]
|
n — число сторон правильного многоугольника - основания правильной пирамиды
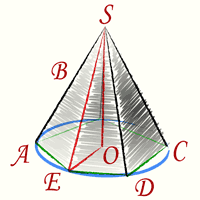
a — сторона правильного многоугольника (AB или BC или CD или DE или EA) - основания правильной пирамиды
h — высота правильной пирамиды (OS)
Боковое ребро правильной пирамиды выводится из следующих формул
Синим цветом на рисунке изображена описанная вокруг основания правильной пирамиды окружность. Треугольник SOE прямоугольный. Его стороны: OS — высота правильной пирамиды (h), OE — радиус описанной окружности вокруг правильного многоугольника (основание правильной пирамиды (R)), SE — Боковое ребро правильной пирамиды (b). По теореме Пифагора
\[ SE = b = \sqrt{ h^2 + R^2 } \]
подставив сюда только радиус описанной окружности получается формула (1).
Вычислить, найти боковое ребро правильной пирамиды по формуле(1)
Боковое ребро правильной пирамиды |
стр. 277 |
|---|
