Радиус вписанной окружности в ромб, формула
Для нахождения радиуса вписанной окружности в ромб произведем следующие геометрические построения:
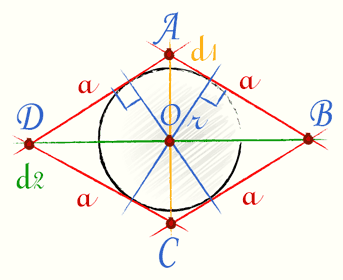
Из рисунка видно, что радиус вписанной окружности в ромб это высота треугольника AOB. У ромба нам известны его диагонали. Соответсвенно через диагонали ромба найдем стороны треугольника AOB. И по классической формуле найдем высоту треугольника т.е. радиус вписанной окружности в ромб.
\[h_a = \frac{ 2 \sqrt{p(p-a)(p-b)(p-c)}}{a}\]
где
\[p=\frac{1}{2}(a+b+c)\]
(a, b, c - стороны треугольника; ha - высота треугольника) У нас
\[b = \frac{d_1}{2}, c = \frac{d_2}{2}, a = \sqrt{\Big(\frac{d_1}{2}\Big)^2+\Big(\frac{d_2}{2}\Big)^2}\]
Вычислить, найти радиус вписанной окружности в ромб по формуле (1)
Радиус вписанной окружности в ромб |
стр. 257 |
|---|
