Радиус вписанной окружности в трапецию, формула
Радиус вписанной окружности в трапецию равен половине высоты трапеции.
\[r=\frac{h}{2}\]
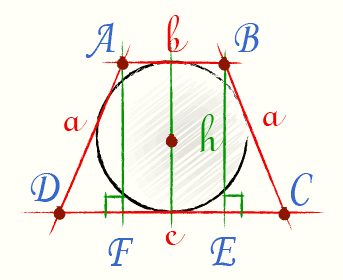Радиус вписанной окружности в трапецию
Главное чтобы выполнялось условие при котором в данную трапецию возможно вписать окружность. В четырехугольник окружность можно вписать только в том случае, если суммы его противоположных сторон равны. т.е.:
\[ AB+DC = AD+BC\]
или
\[ 2a = b+c\]
Иначе в данную трапецию нельзя вписать окружность.
бедро трапеции выражается через высоту по теореме Пифагора:
\[ BC = a = \sqrt{h^2 + \Big(\frac{c-b}{2}\Big)^2} \]
Отсюда — зная все стороны трапеции вычислим такую высоту трапеции, которая удовлетворяет условию вписанной окружности (3).
\[b+c = 2 \sqrt{h^2 + \Big(\frac{c-b}{2}\Big)^2}\]
после небольших преобразований получим
\[h = \sqrt{ \Big(\frac{c+b}{2}\Big)^2 - \Big(\frac{c-b}{2}\Big)^2}\]
\[h = \frac{1}{2} \sqrt{ (c+b)^2 - (c-b)^2}\]
используем формулы Квадрат суммы и Квадрат разности и после раскрытия скобок и упрощения получим
\[h=\sqrt{bc}\]
И соответственно радиус вписанной окружности в трапецию
\[r=\frac{h}{2}=\frac{\sqrt{bc}}{2}\]
Вычислить, найти радиус вписанной окружности в трапецию по формуле (1,2,3,4,5)
Радиус вписанной окружности в трапецию |
стр. 259 |
|---|
