Радиус вписанной окружности равнобедренного треугольника, формула
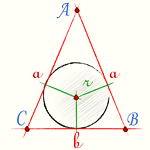Радиус вписанной окружности равнобедренного треугольника вычисляется по классической формуле
\[r = \sqrt{\frac{(p-a)(p-a)(p-b)}{p}}\]
где
\[p=\frac{1}{2}(a+a+b)=a+\frac{b}{2}\]
(a, b - стороны равнобедренного треугольника;
r - радиус вписанной окружности равнобедренного треугольника)
После подстановок, преобразований и упрощений получается следующая формула:
\[r = \frac{b}{2} \sqrt{ \frac{2a-b}{2a+b} } \]
Вычислить, найти радиус вписанной окружности равнобедренного треугольника по формуле (3)
Радиус вписанной окружности равнобедренного треугольника |
стр. 261 |
|---|
