Радиус описанной окружности трапеции, формула
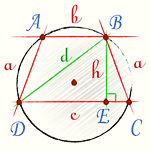Для нахождения радиуса описанной окружности трапеции делают дополнительные построения — строят диагональ трапеции — BD.
Теперь трапеция разбита на два треугольника ABD и BСD. Окружность при этом описана вокруг обоих этих треугольников. Далее по известным параметрам трапеции находим недостающие стороны этих треугольников и по классической формуле радиуса описанной окружности треугольника находим радиус описанной окружности трапеции:
\[R = \frac{adc}{4\sqrt{p(p-a)(p-d)(p-c)}}\]
где
\[p=\frac{1}{2}(a+d+c)\]
(a (BC), d (BD), c (CD) - стороны треугольника; R - радиус описанной окружности треугольника)
Пусть у нашей равнобокой трапеции заданы основания и высота (см. рисунок ниже), тогда:
\[ EC = \frac{c-b}{2} \\ \medspace \\ DE = c - \frac{c-b}{2} = \frac{c+b}{2} \]
по теореме Пифагора найдутся диагональ:
\[ BD = d = \sqrt{h^2 + \Big(\frac{c+b}{2}\Big)^2} \]
и бедро трапеции:
\[ BC = a = \sqrt{h^2 + \Big(\frac{c-b}{2}\Big)^2} \]
Вычислить, найти радиус описанной окружности трапеции по формулам (1,2,3,4,5)
Радиус описанной окружности трапеции |
стр. 250 |
|---|
