Радиус описанной окружности шестиугольника, формула
Для расчета радиуса описанной окружности шестиугольника используем формулу радиуса описанной окружности правильного многоугольника
\[R = \frac{a}{2 \sin(\frac{360°}{12})} = \frac{a}{2 \sin(30°)} = a\]
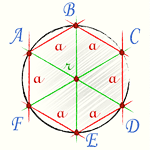
(a - сторонa правильного шестиугольника; R - радиус описанной окружности правильного шестиугольника) Также можно пойти другим путем. Если соединить все вершины правильного шестиугольника через центр, станет видно, что правильный шестиугольник состоит из 6-ти правильных треугольников, т.е.
\[R = \frac{a}{2 \sin(π/6)} = a\]
Вычислить, найти радиус описанной окружности шестиугольника по формуле (2)
Радиус описанной окружности шестиугольника |
стр. 253 |
|---|
