Правильный семиугольник
Правильный семиугольник — это такой семиугольник у которого все семь сторон равны и его семь углов равны.
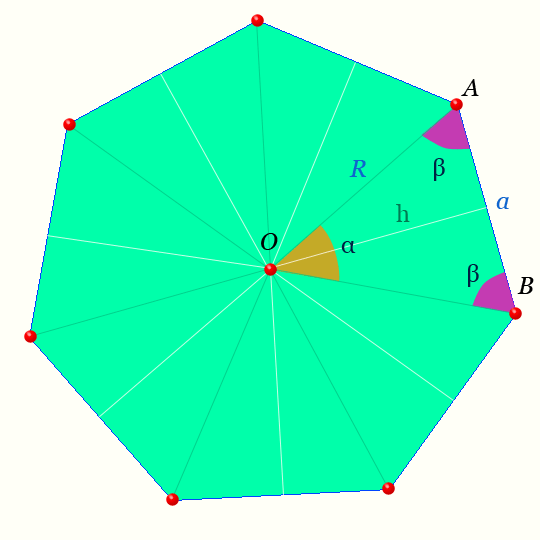
Правильный семиугольник
Центр правильного семиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA, OB — радиусы правильного семиугольника.
Обозначения на рисунке для правильного семиугольника
| n=7 | число сторон и вершин правильного семиугольника, | шт |
|---|---|---|
| α | центральный угол правильного семиугольника, | радианы, ° |
| β | половина внутреннего угла правильного семиугольника, | радианы, ° |
| γ | внутренний угол правильного семиугольника, | радианы, ° |
| a | сторона правильного семиугольника, | м |
| R | радиусы правильного семиугольника, | м |
| p | полупериметр правильного семиугольника, | м |
| L | периметр правильного семиугольника, | м |
| h | апофемы правильного семиугольника, | м |
Основные формулы для правильного семиугольника
Периметр правильного семиугольника
\[ L = 7a \]
Полупериметр правильного семиугольника
\[ p = \frac{7}{2}a \]
Центральный угол правильного семиугольника в радианах
\[ α = \frac{2}{7}π \]
Центральный угол правильного семиугольника в градусах
\[ α = \frac{2}{7}180° = ~51.428571° \]
Половина внутреннего угла правильного семиугольника в радианах
\[ β = \frac{5}{14}π \]
Половина внутреннего угла правильного семиугольника в градусах
\[ β = \frac{5}{14}180° = ~64.28571° \]
Внутренний угол правильного семиугольника в радианах
\[ γ = 2β = \frac{5}{7}π \]
Внутренний угол правильного семиугольника в градусах
\[ γ = \frac{5}{7}180° = ~128.57142° \]
Площадь правильного семиугольника
\[ S = ph = \frac{7}{2}ha \]
Правильный семиугольник |
стр. 271 |
|---|
