Биссектриса треугольника, формула
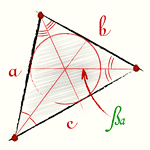Биссектриса треугольника, это отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороной. Три биссектрисы треугольника всегда пересекаются в одной точке всегда внутри треугольника, эта точка является центром вписанного круга. Биссектриса угла A обозначается βa
\[ β_a = \frac{2}{b+c} \sqrt{bcp(p-1)} \]
где
\[p=\frac{1}{2}(a+b+c)\]
(a, b, c - стороны треугольника; βa - биссектриса треугольника) Биссектриса делит противоположную сторону на части, пропорциональные прилежащим к ней сторонам AE:EC = AB:BC
Вычислить, найти биссектрису треугольника по формуле (1)
Биссектриса треугольника |
стр. 235 |
|---|
