Высота равнобедренного треугольника, формула
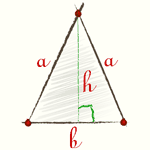 |
Формулу высоты равнобедренного треугольника можно получить из теоремы Пифагора, а также по формуле Герона |
Высота равнобедренного треугольника из теоремы Пифагора, формула
\[
h^2+\Big(\frac{b}{2}\Big)^2=a^2 \\
h^2=a^2-\Big(\frac{b}{2}\Big)^2
\]
\[
h=\sqrt{a^2-\frac{b^2}{4}}
\]
Высота равнобедренного треугольника по формуле Герона, формула
\[
h = \frac{ 2 \sqrt{p(p-a)(p-b)(p-a)}}{b}
\]
где
\[
p=\frac{1}{2}(a+b+a)=a+\frac{b}{2}
\]
после подстановки коэффициента p в формулу получим
\[
h = \frac{ 2 \sqrt{(a+\frac{b}{2})(a+\frac{b}{2}-a)(a+\frac{b}{2}-b)(a+\frac{b}{2}-a)}}{b}
\]
\[
h = \frac{ 2 \sqrt{(a+\frac{b}{2})(\frac{b}{2})(a-\frac{b}{2})(\frac{b}{2})}}{b}
\]
по формулам сокращенного умножения, разность квадратов получим
\[
\Big(a+\frac{b}{2}\Big)\Big(a-\frac{b}{2}\Big)=a^2-\Big(\frac{b}{2}\Big)^2
\]
далее вносим под корень 2 и знаменатель b
\[
h = \sqrt{\frac{2^2(a^2-(\frac{b}{2})^2)(\frac{b}{2})^2}{b^2}}
\]
после сокращений получим
\[
h=\sqrt{a^2-\frac{b^2}{4}}
\]
Вычислить, найти высоту равнобедренного треугольника по формуле (9)
Высота равнобедренного треугольника |
стр. 232 |
|---|
