Боковая поверхность правильной усеченной пирамиды, формула
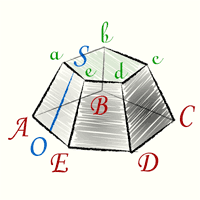Правильная усеченная пирамида — это многогранник, у которого одна грань — основание пирамиды — правильный многоугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины.
Сечение параллельное основанию пирамиды делит пирамиду на две части. Часть пирамиды между ее основанием и этим сечением — это усеченная пирамида.
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему:
\[ S_{бок} = \frac{1}{2} (p_1 + p_2) a \]
p1 — периметр нижнего основания правильной усеченной пирамиды (ABCDE)p2 — периметр верхнего основания правильной усеченной пирамиды (abcde)
a — апофема правильной усеченной пирамиды (OS)
Вычислить, найти боковую поверхность правильной усеченной пирамиды по формуле(1)
Боковая поверхность правильной усеченной пирамиды |
стр. 328 |
|---|
