Площадь поверхности шарового сектора, формула
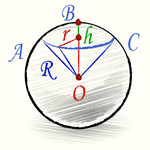
Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью основанием которой служит основание сегмента, а вершиной — центр шара.
Поверхность шарового сектора складывается из кривых поверхностей шарового сегмента и конуса. Зная радиус основания сегмента и конуса r при помощи теоремы Пифагора и прямоугольного треугольника получим высоты сегмента и конуса:
\[ h_{конуса} = \sqrt{R^2-r^2} \]
\[ h_{сегмента} = R - \sqrt{R^2-r^2} \]
Подставим формулы площади конуса и шарового сегмента:
\[ S_{сектора} = S_{сегмента} + S_{конуса} \]
\[ S_{сектора} = 2 \pi R h_{сегмента} + \pi R r \]
\[ S_{сектора} = \pi R ( 2 (R - \sqrt{R^2-r^2}) + r ) \]
Формулы шара, сферы
Площадь поверхности сферы
Объем шара
Площадь поверхности шарового сегмента
Объем шарового сегмента
Площадь поверхности шарового слоя
Объем шарового слоя
Объем шарового сектора
Вычислить, найти площадь поверхности шарового сектора по формуле (5)
Площадь поверхности шарового сектора |
стр. 317 |
|---|
