Площадь сектора круга, окружности, формула
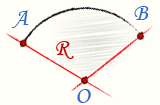Сектор круга, окружности — это часть круга, окружности ограниченная дугой и двумя радиусами, проведенными к концам дуги.
Площадь сектора круга через длину дуги сектора
Площадь сектора круга равна произведению половины длины дуги сектора p на радиус круга.
\[ S = \frac{1}{2}pr \]
Вычислить, найти площадь сектора круга через длину дуги сектора по формуле (1)
Площадь сектора круга через угол сектора в градусах
Площадь сектора круга с дугой n° равна произведению площади окружности с радиусом r на отношение угла сектора n° к углу полной окружности, т.е. 360°
\[ S = \pi r^2 \frac{n°}{360°} \]
Вычислить, найти площадь сектора круга через угол сектора в градусах по формуле (2)
Площадь сектора круга через угол сектора в радианах
Площадь сектора круга с дугой α радиан равна произведению квадрата радиуса на половину угла
\[ S = \frac{α}{2}r^2 \]
Вычислить, найти площадь сектора круга через угол сектора в радианах по формуле (3)
Площадь сектора круга |
стр. 308 |
|---|
