Площадь треугольника через углы, формула
Площадь треугольника через две стороны и угол между ними, формула
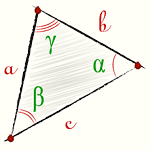
Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними.
\[ S = \frac{1}{2} a b \sin(γ) \]
\[ S = \frac{1}{2} a c \sin(β) \]
\[ S = \frac{1}{2} b c \sin(α) \]
Площадь треугольника через одну сторону и прилежащие к ней углы, формула
Если известна одна сторона треугольника и два прилежащих к ней угла, то площадь данного треугольника вычисляется, как половина квадрата данной стороны умноженная на дробь, в числителе которой, произведение синусов прилежащих углов, а в знаменателе синус противолежащего угла. Противолежащий угол вычисляется по формуле:
\[ γ = 180° - (α + β) \]
\[ β = 180° - (α + γ) \]
\[ α = 180° - (β + γ) \]
Площадь треугольника вычисляется по формулам:
\[ S = \frac{1}{2} a^2 \frac{\sin(β)\sin(γ)}{\sin(α)} \]
\[ S = \frac{1}{2} b^2 \frac{\sin(α)\sin(γ)}{\sin(β)} \]
\[ S = \frac{1}{2} c^2 \frac{\sin(α)\sin(β)}{\sin(γ)} \]
Ссылки по теме
Формула площади прямоугольного треугольникаПлощадь равнобедренного треугольникаКак вычислить площадь равностороннего треугольникаОбщая формула площади треугольникаФормула Герона
Площадь треугольника через углы |
стр. 303 |
|---|
