Формулы и расчеты онлайн - Fxyz.ru

← Назад	Вперед →

Модуль и аргумент комплексного числа, формулы

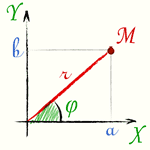Длина вектора, изображающего комплексное число, называется модулем комплексного числа. Модуль любого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + i·b обозначается |a + i·b|, а также буквой r. Из чертежа видно, что:

\[r = \vert a + \htmlStyle{color: MediumPurple;}{i} b \vert = \sqrt{a^2+b^2}\]

Модуль действительного числа, совпадает с его абсолютным значением. Сопряженные комплексные числа a + i·b и a - i·b имеют один и тот же модуль.

Угол φ между осью абсцисс и вектором OM, изображающим комплексное число a + i·b, называется аргументом комплексного числа a + i·b

Каждое не равное нулю комплексное число имеет бесчисленное множество аргументов, отличающихся друг от друга на целое число полных оборотов (т.е. на 360°·k, где k - любое целое число). Аргумент комплексного числа связан с его координатами следующими формулами:

\[ \tg(φ) = \frac{b}{a} \]

\[ \cos(φ) = \frac{a}{\sqrt{a^2+b^2}}\]

\[ \sin(φ) = \frac{b}{\sqrt{a^2+b^2}}\]

Однако ни одна из этих формул в отдельности не позволяет найти аргумент. Для того чтобы найти аргумент комплексного числа, эти формулы надо использовать в совокупности, а также учитывать номер четверти, на координатной плоскости, в которой находится комплексное число.