Тригонометрическая форма комплексного числа, формула
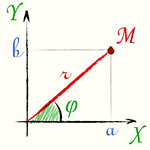Абсцисса a и ордината b комплексного числа a + i·b выражаются через модуль r и аргумент φ формулами:
\[a = r \cdot \cos(φ)\]
\[b = r \cdot \sin(φ)\]
Поэтому всякое комплексное число можно представить в виде:
\[ a + \htmlStyle{color: MediumPurple;}{i}b = r \cdot (\cos(φ) + \htmlStyle{color: MediumPurple;}{i}\sin(φ))\]
Это так называемая, нормальная тригонометрическая форма, или просто, тригонометрическая форма комплексного числа.
В противоположность тригонометрической форме выражение вида a + i·b называется алгебраической или координатной формой комплексного числа.
Выразить комплексное число в тригонометрической форме по формулам (1, 2, 3)
Тригонометрическая форма комплексного числа |
стр. 76 |
|---|
