Формулы и расчеты онлайн - Fxyz.ru

← Назад	Вперед →

Матрицы

Матрицы — это прямоугольные таблицы из чисел, содержащие m строк и n столбцов.

Числа m и n называются порядками матрицы.

Запись матриц

Матрицы записываются с помощью больших круглых скобок

\[ \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \dots & \dots & \dots & \dots \\ a_{m1} & a_{m2} & \dots & a_{mn} \\ \end{pmatrix} \]

Для краткого обозначения матрицы используется большая латинская буква, например A, или символ a_i,j или подробно

\[ A = a_{i,j} = (a_{i,j})\begin{cases} i={1,2,\dots,m} \\ j={1,2,\dots,n} \end{cases} \]

Элементы матрицы

Числа a_i,j, входящие в состав матрицы, называются ее элементами. Здесь i — номер строки матрицы, j — номер столбца матрицы.

Квадратные матрицы

Если

\[ m = n \]

то матрицы называются квадратными

\[ \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \dots & \dots & \dots & \dots \\ a_{n1} & a_{n2} & \dots & a_{nn} \\ \end{pmatrix} \]

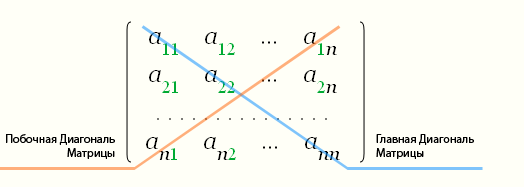
Главная диагональ матрицы

Главной диагональю матрицы называется диагональ

\[a_{11} \quad a_{22} \quad \dots \quad a_{nn}\]

идущая из левого верхнего угла в правый нижний угол.

Побочная диагональ матрицы

Побочной диагональю матрицы называется диагональ

\[a_{n1} \quad a_{(n-1)2} \quad \dots \quad a_{1n}\]

идущая из левого нижнего угла в правый верхний угол.

Равенство матриц

Две матрицы равны, если эти матрицы имеют одинаковые размеры, и все их соответствующие элементы совпадают.

Действия над матрицами и типы матриц

Матрицы	стр. 128


e	π	g	C
sin	cos	tan	√	exp
asin	acos	atan	lg	ln
7	8	9	(	)
4	5	6	×	÷
1	2	3	+	-
0	.	=

Матрицы

Запись матриц

Элементы матрицы

Квадратные матрицы

Главная диагональ матрицы

Побочная диагональ матрицы

Равенство матриц

Действия над матрицами и типы матриц

Матрицы

Подтемы

См. также

Разделы

Калькулятор

Дополнительно