Ограниченная величина
Ограниченная величина это такая величина, абсолютное значение которой не превосходит некоторого (постоянного) положительного числа М.
\[ f(x) = \sin(x) \]
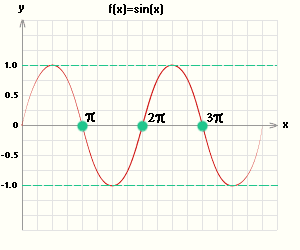
Ограниченная величина
Функция $ f(x) = \sin(х) $ — ограниченная величина на всей числовой оси, поскольку
\[ \lvert \sin(x) \rvert \leqslant 1 \]
\[ f(x) = \frac{1}{x-2} \]
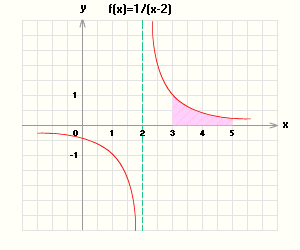
Ограниченная величина
Функция $ f(x)=1/(x-2) $ ограничена в промежутке (3, 5), но не ограничена в промежутке (2,5), поскольку аргумент х, оставаясь в промежутке (2, 5), может стремиться к 2, а тогда функция бесконечно велика.
Всякая постоянная величина является ограниченной.
Всякая бесконечно большая величина не ограничена.
Ограниченная величина |
стр. 176 |
|---|

Так, целочисленная функция
При нечетных n она всегда равна нулю.
Но она и не ограничена, поскольку при четных n, начиная с некоторого номера, остается больше любого положительного числа М.