Строфоида
Строфоиду в 1645 году впервые изучал французский ученый Г.Персонье (1602 — 1675). В его трудах эта линия называлась птероида от греческого птербн (πτερον) — крыло.
Персонье родился в деревне Роберваль и поэтому взял себе созвучный псевдоним. Он изобрел весы, которые назвали его именем, а также заложил основы метода бесконечно малых величин.
Современное название этой линии, Строфоида, происходит от греческого слова строфе (στροφη) — поворот, а предложил его математик Миди в 1849 г.
Определение и построение строфоиды
Прямая строфоида
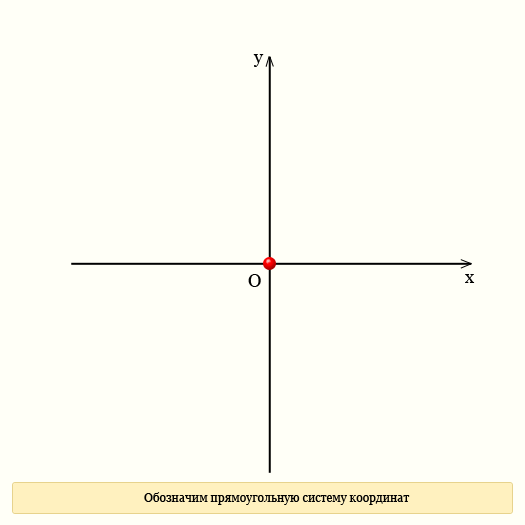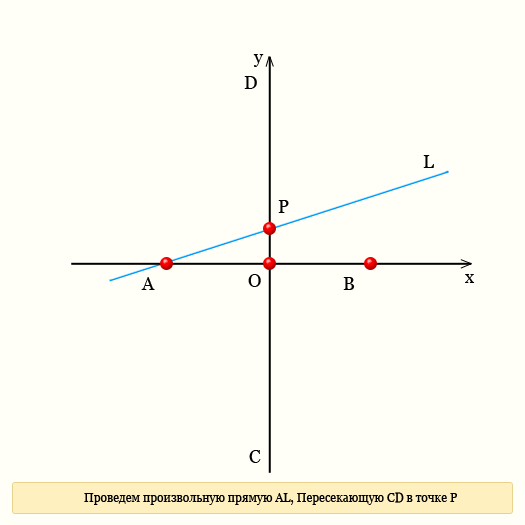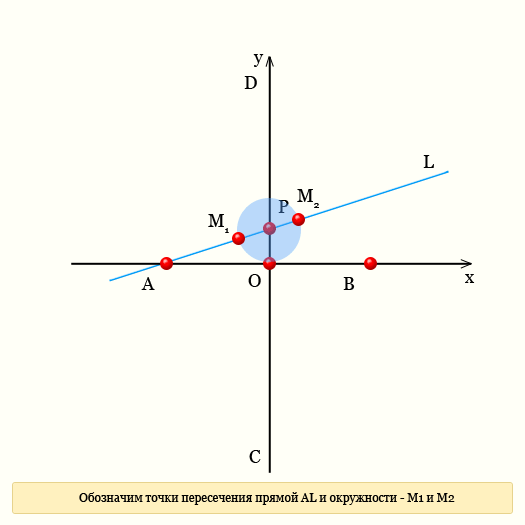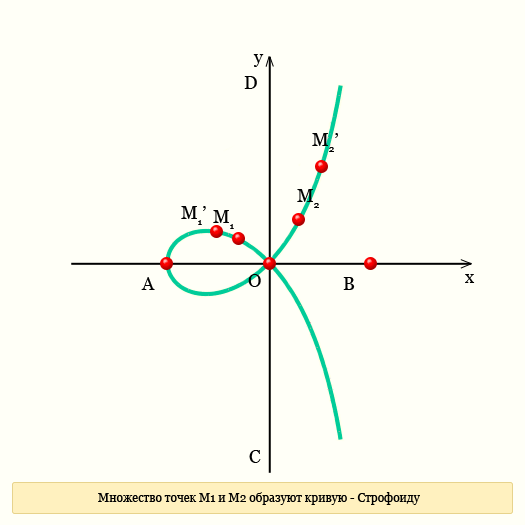
Чтобы построить прямую строфоиду или просто строфоиду, необходимо провести взаимно-перпендикулярные прямые АВ и CD. Обозначим точку пересечения AB и CD буквой O. Через точку А провести прямую произвольно, в любом направлении, чтобы эта прямая пересекла CD в некоторой точке P. назовем эту прямую AL. Измеряем расстояние от точки P до точки O, и проводим циркулем радиус PO. Там где окружность пересекается с прямой AL поставим точки M1 и M2.
Прямая строфоида —
геометрическое место точек M1 и M2.
Косая строфоида
Косая строфоида строится аналогично прямой строфоиде, но АВ и CD пересекаются не под прямым углом.
Стереометрическое образование
Прямая строфоида
Дан цилиндр. Его ось CD. Его радиус AO. Плоскость К перпендикулярна чертежу и проходит через точку A. Прямая AL след плоскости K. Сечение цилиндра плоскостью K есть эллипс. Фокусы эллипса M1, M2 описывают прямую строфоиду.
Косая строфоида
Строится аналогично, но цилиндр заменяется конусом. Ось конуса OS перпендикулярна к AB. Прямая UV, проходит через B параллельно CD, — одна из образующих. Плоскость К перпендикулярна чертежу и проходит через точку A. Прямая AL след плоскости K. Сечение конуса плоскостью K есть эллипс. Точки M1, M2 - фокусы сечения. Косая строфоида расположена на обеих полостях конической поверхности и проходит через вершину S.
Уравнение строфоиды в декартовой системе
O — начало, ось ОХ направлена по лучу ОВ, АО = а, угол AOD = α. когда строфоида — косая, система координат — косоугольная. ось OY направлена по лучу OD:
Для прямой строфоиды уравнение приводится к виду:
Уравнение строфоиды в полярной системе
O — полюс, ОХ — полярная ось:
Рациональное параметрическое представление
(u = tg(φ)):
Особенности строфоиды
Точка О узловая. Касательные к двум ветвям, проходящим через О, взаимно перпендикулярны и для прямой, и для косой строфоиды. Прямая UV — асимптота для косой строфоиды (при бесконечном удалении вниз). Также UV касается косой строфоиды в точке S, равноотстоящей от А и В.
У прямой строфоиды точка касания S «уходит в бесконечность» (при удалении вверх), так что прямая UV служит асимптотой для обеих ветвей.
Радиус кривизны в узловой точке прямой строфоиды
Площадь петли AOM прямой строфоиды
Объем тела, произведенного вращением петли AOM вокруг оси OX
Площадь, между ветвями OU`, OV` и асимптотой
Эта площадь простирается в бесконечность, но имеет конечную величину.
Объем тела, произведенного вращением фигуры U`OV`VU около оси ОХ
Имеет бесконечную величину.
Строфоида |
стр. 126 |
|---|
