Ускорение незатухающих гармонических колебаний, формула
Гармонические колебания представляют собой движение с переменным ускорением, т. е. ускорение не постоянно, а является функцией времени:
Ускорение незатухающих гармонических колебаний
\[
a = a(t)
\]
Если
| a | мгновенное ускорение, | метр / секунда2 |
|---|---|---|
| Am | максимальное ускорение в точке поворота (амплитуда ускорения), | метр / секунда2 |
| ω | угловая частота, | радиан / секунда |
| f | линейная частота, | Герц |
| φ | фаза, | радиан |
| t | время, | секунда |
то,
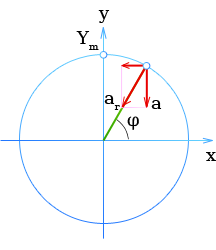
Поскольку мгновенное ускорение колебательной системы всегда равно вертикальной составляющей центростремительного ускорения,
\[
a_{r} = Y_{m} ω^2
\]
в соответствии с рисунком получаем
\[
\sin(φ) = \frac{a}{Y_{m} ω^2}
\]
Согласно
\[
a = \frac{d\differential{y}}{dt} = \frac{d^2 y}{dt} = \doubledifferential{y}
\]
Из обоих выражений следует
\[
a = -Y_{m} ω^2 \sin(φ) = A_{m} \sin(φ) = - ω^2 y
\]
В точке поворота φ = 90º или 270º; тогда sin(φ) = ±1 и формула (5) принимает вид
\[
A_{m} = -Y_{m} ω^2
\]
Знак минус свидетельствует о том, что ускорение направлено противоположно отклонению, т. е. направлено всегда к положению равновесия.
Ускорение незатухающих гармонических колебаний |
стр. 541 |
|---|
