Фаза незатухающих гармонических колебаний, формула
Гармонические колебания — это колебание проекции точки двигающейся равномерно по окружности на прямую.
Если построить график отклонения точки от нуля в зависимости от угла поворота точки по окружности получится график функции синус, или синусоида.
Угол поворота точки по окружности при равномерном вращении пропорционален времени. Соответственно фаза гармонического колебания это угол, соответствующий времени.
Для любых колебаний отклонение у, мгновенная скорость u и мгновенное ускорение a являются функциями времени t, а также фазы φ поскольку φ = ωt.
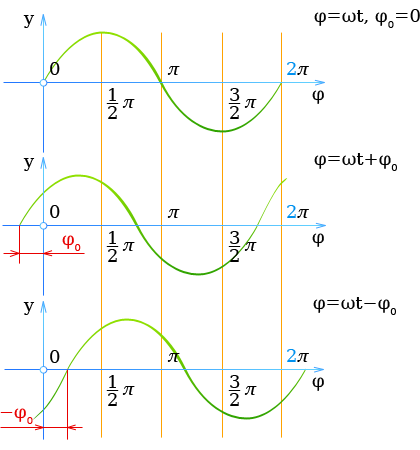
При определении фазы необходимо учитывать начальную фазу φ0, т. е. значение фазы в начальный момент (t = 0).
Если
| φ | фаза, | радиан |
|---|---|---|
| φ0 | начальная фаза, | радиан |
| ω | круговая частота, | радиан / секунда |
| f | линейная частота, | Герц |
| t | время, | секунда |
то выполняется соотношение
Фаза в (1) всегда получается в радианах. Cм. пересчет радиан в градусы.
Найти, вычислить фазу колебаний по формуле (1) через круговую частоту ω
Найти, вычислить фазу колебаний по формуле (1) через линейную частоту f
Фаза незатухающих гармонических колебаний |
стр. 538 |
|---|
