Формулы и расчеты онлайн - Fxyz.ru

← Назад	Вперед →

Энергия незатухающих гармонических колебаний, формула

Энергия системы, колеблющейся без затухания (энергия незатухающих гармонических колебаний), остается постоянной. Она складывается из потенциальной энергии W_п и кинетической энергии W_к. Величины обеих энергий меняются периодически, но в каждый момент

\[ W = W_{п} + W_{к} \]

Используя формулы потенциальной и кинетической энергий, получаем

\[ W = \frac{Dy^2}{2} + \frac{mu^2}{2} \]

Если

W	энергия колебательной системы,	Джоуль
D	жесткость,	Ньютон / метр
Y_m	амплитуда, максимальное отклонение,	метр
ω	угловая частота,	радиан / секунда
f	линейная частота,	Герц
φ	фаза,	радиан

то, используя формулы отклонения и скорости, получаем

\[ W = \frac{D}{2} Y_{m}^2 \sin^2(φ) + \frac{m}{2} Y_{m}^2 ω^2 \cos^2(φ) \]

Поскольку

\[ ω^2 = \frac{D}{m} \]

имеем

\[ W = \frac{D}{2} Y_{m}^2 \sin^2(φ) + \frac{D}{2} Y_{m}^2 \cos^2(φ) \]

и окончательно

\[ W = \frac{D}{2} Y_{m}^2 (\sin^2(φ) + \cos^2(φ)) \]

\[ W = \frac{D}{2} Y_{m}^2 = \frac{m}{2} V_{m}^2 \]

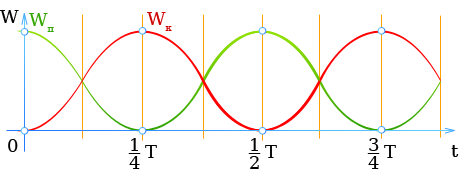
Энергия незатухающих гармонических колебаний

В процессе колебаний потенциальная энергия превращается в кинетическую и наоборот. При этом полная энергия остается постоянной. Процесс перехода энергии из одного вида в другой носит периодический характер.
В точке поворота и при прохождении положения равновесия энергия одного вида равна нулю, в то время как энергия другого вида достигает максимума.