Отклонение затухающих колебаний, формула
Если
| y | отклонение, | метр |
|---|---|---|
| y0 | начальная амплитуда, | метр/сек |
| e = 2.718 | основание натуральных логарифмов, | |
| δ = β/2m | коэффициентом затухания, | 1/сек |
| t | время, | сек |
| ωзат | круговая частота затухающих колебаний, | радиан/сек |
| φ0 | начальная фаза, | радиан |
| φ | фаза, | радиан |
\[
φ = ω_{зат}t + φ_0
\]
то решение дифференциального уравнения затухающих колебаний имеет вид
\[
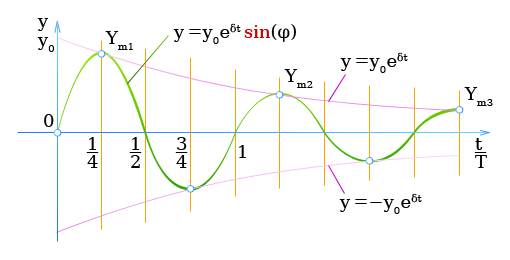
y = y_0 e^{-δt} \sin(φ)
\]
Амплитуда экспоненциально уменьшается со временем.
Отношение двух последовательных значений амплитуды остается постоянным. Эти численные значения амплитуд образуют убывающую геометрическую прогрессию.
Если
| k | отношение амплитуд, | |
|---|---|---|
| δ = β/2m | коэффициентом затухания, | 1/сек |
| T | период затухающих колебаний, | сек |
| Λ | логарифмический декремент, | |
| n | любое целое число, |
то
\[
\frac{Y_{m, i}}{Y_{m, i+1}} = k
\]
Следовательно, n-я амплитуда определяется формулой
\[
Y_{m, i+1} = \frac{Y_{m, i}}{k^n}
\]
Поскольку промежуток времени между двумя последовательными амплитудами равен периоду Т, получаем
\[
e^{δT} = \frac{Y_{m, i}}{Y_{m, i+1}}
\]
Или
\[
e^{n δT} = \frac{Y_{m, i}}{Y_{m, i+1}}
\]
Показатель экспоненты δТ называется логарифмическим декрементом Λ. Логарифмирование формулы дает
\[
Λ = δT = \ln\bigg(\frac{Y_{m, i}}{Y_{m, i+1}}\bigg)
\]
Логарифмический декремент Λ представляет собой натуральный логарифм отношения амплитуд k.
Отклонение затухающих колебаний |
стр. 552 |
|---|
