Связанные колебания
Связанные колебательные системы влияют друг на друга. Колебания таких систем уже не будут независимы, поскольку системы обмениваются энергией. Связь может быть обусловлена:
- упругостью
- трением
- инерцией
Если одной из систем сообщили энергию и она совершает колебательное движение, то постепенно она передает свою энергию второй системе. Скорость передачи энергии зависит от того, насколько сильна связь, т. е. от степени связи χ.
Если у обеих систем одинаковая собственная частота, то после того, как система 1 придет в состояние покоя (ее энергия обратится в нуль), изменится направление потока энергии. Обе системы будут совершать биения, сдвинутые по времени на Тб/2.
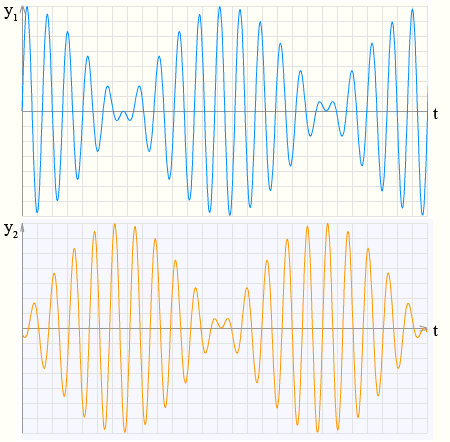
Биения возникают в результате сложения собственных (нормальных) колебаний обеих систем.
Имеются два возможных типа колебаний связанных систем, при которых устанавливается обмен энергией:
- Системы колеблются в фазе (синфазно). Наличие связи не меняет частоты, и обе системы колеблются с частотой f1 = f0.
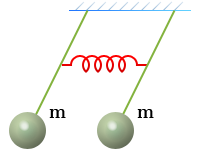Связанные колебания — Системы колеблются в фазе - Системы колеблются в противофазе (∆φ = π). Из-за дополнительной жесткости Dсв, обусловленной наличием связи, частота колебаний уменьшается. Обе системы колеблются в этом случае с частотой f2.
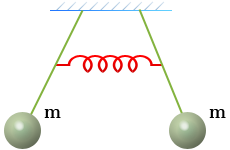Связанные колебания — Системы колеблются в противофазе
Если
| D | жесткость системы 1, равная жесткости системы 2, | Ньютон / метр |
|---|---|---|
| Dсв | дополнительная жесткость, обусловленная связью, | Ньютон / метр |
| m | масса системы 1, равная массе системы 2, | кг |
то
то для частот f1 и f2 собственных колебаний получаем
Жесткости систем или периоды Т = 1/f собственных колебаний определяют степень связи.
Выражения (1), (2) и (3) справедливы только для случая, когда массы, собственные частоты и жесткости систем одинаковы.
Связанные колебания |
стр. 567 |
|---|
