Изменение объема при нагревании, первый закон Гей-Люссака
Если
| Vt | объем газа при произвольной температуре t, | метр3 |
|---|---|---|
| V0 | объем газа при температуре 0°С, | метр3 |
| t | температура, | 0°С |
| β | коэффициент объемного расширения газа, | 1/K |
то
\[ V_t = V_0 ( 1 + βt ) \]
Из формулы (1) следует, что при температуре t1
\[ V_1 = V_0 ( 1 + βt_1 ) \]
\[ V_1 = V_0 \bigg( 1 + \frac{t_1}{273.15} \bigg) \]
\[ V_1 = V_0 \bigg( 1 + \frac{t_1}{T_0} \bigg) \]
\[ V_1 = V_0 \bigg( \frac{T_0 + t_1}{T_0} \bigg) \]
а при другой температуре t2 соответственно
\[ V_2 = V_0 ( 1 + βt_2 ) \]
\[ V_2 = V_0 \bigg( 1 + \frac{t_2}{273.15} \bigg) \]
\[ V_2 = V_0 \bigg( 1 + \frac{t_2}{T_0} \bigg) \]
\[ V_2 = V_0 \bigg( \frac{T_0 + t_2}{T_0} \bigg) \]
Разделив первое равенство на второе, получим
\[ \frac{V_1}{V_2} = \frac{T_0 + t_1}{T_0 + t_2} \]
или
\[ \frac{V_1}{V_2} = \frac{T_1}{T_2} \]
или
\[ \frac{V}{T} = \const \]
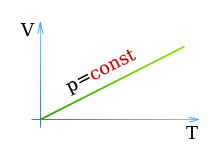
Первый закон Гей-Люссака
Первый закон Гей-Люссака гласит: При постоянном давлении объем газа V пропорционален абсолютной температуре газа T
\[ V \sim T \qquad (\enspace p = \const \enspace) \]
Формула (11) справедлива только для идеальных газов, для реальных газов она является хорошим приближением и неприменима в случае пара.
Изменение объема при нагревании, первый закон Гей-Люссака |
стр. 523 |
|---|
