Емкость сферического конденсатора
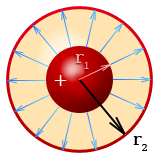
Сферический конденсатор состоит из двух концентрических полых сфер. Если расстояние между сферами ∆r очень мало, так что площадь обеих сферических поверхностей практически одинакова, то можно пользоваться выражением для емкости плоского конденсатора. Полагая S = 4πr2 см. площадь сферы, получаем:
\[ C = 4 π ε_{0} ε \frac{r^2}{∆r} \]
При большем расстоянии между поверхностями нужно учитывать различие площадей сфер.
Если
| C | емкость сферического конденсатора, | фарад |
|---|---|---|
| r1 | радиус внутренней сферы, | метр |
| r2 | радиус внешней сферы, | метр |
| εa | εa=ε0ε абсолютная диэлектрическая проницаемость, | Фарад/метр |
| ε0 | ε0=8.85·10-12электрическая постоянная, | Фарад/метр |
| ε | относительная диэлектрическая проницаемость, |
то
\[ C = 4 π ε_{0} ε \frac{r_1 r_2}{r_2 - r_1} \]
Вычислить найти емкость сферического конденсатора по формуле (2)
Емкость сферического конденсатора |
стр. 635 |
|---|
