Формулы и расчеты онлайн - Fxyz.ru

← Назад	Вперед →

Радиальное (нормальное) ускорение

При движении тела по криволинейной траектории возникает радиальное ускорение. Оно всегда перпендикулярно направлению мгновенной скорости.

Радиальное (нормальное) ускорение равно квадрату угловой скорости помноженному на радиус траектории (5).

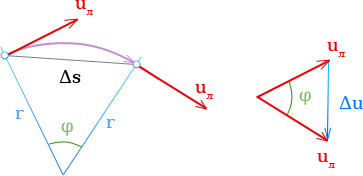
Для достаточно малого промежутка времени Δt справедливы следующие соотношения:

\[ \frac{Δs}{r} = \frac{Δu}{u_{л}} \]

Так как

\[ Δs = u_{л} Δt \]

имеем

\[ \frac{Δu}{u_{л}} = \frac{u_{л} Δt}{r} \]

или

\[ \frac{Δu}{Δt} = \frac{u_{л}^2}{r} \]

Отсюда получается радиальное ускорение

\[ a_{р} = \frac{u_{л}^2}{r} = ω^2 r \]

Радиальное ускорение меняет только направление, но не величину скорости.

Тот же результат можно получить рассмотрев координаты лежащей на окружности точки Р, в которой в данный момент находится тело:

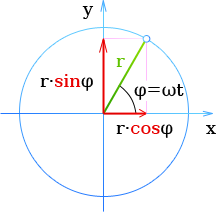
Радиальное (нормальное) ускорение в декартовых координатах

\[ \begin{cases} x = r \cos(φ) \\ y = r \sin(φ) \end{cases} \]

Из выражения Равномерное движение тела по окружности [1] следует

\[ φ = ωt \]

Согласно формуле Мгновенное ускорение [2] ускорение представляет собой вторую производную перемещения по времени. Продифференцировав дважды координаты точки Р, найдем ускорения в направлении осей координат:

\[ \begin{cases} \dot{x} = -ωr \sin(ωt) \\ \dot{y} = ωr \cos(ωt) \end{cases} \]

\[ \begin{cases} \ddot{x} = -ω^2 r \cos(ωt) \\ \ddot{y} = -ω^2 r \sin(ωt) \end{cases} \]

Знаки минус указывают на то, что ускорение направлено к началу координат.

Отсюда для результирующего ускорения имеем

\[ a_p^2 = (− ω^2 r \cos(ωt))^2 + (− ω^2 r \sin(ωt))^2 \]

\[ a_p^2 = ω^4 r^2 (\cos^2(ωt) + \sin^2(ωt)) \]

\[ a_p = \sqrt{ω^4 r^2} = ω^2 r \]

таким образом (11) и (5) совпадают.

Вычислить, найти радиальное (нормальное) ускорение по формуле (5) через линейную скорость

Вычислить, найти радиальное (нормальное) ускорение по формуле (5) через угловую скорость

Радиальное (нормальное) ускорение	стр. 436


e	π	g	C
sin	cos	tan	√	exp
asin	acos	atan	lg	ln
7	8	9	(	)
4	5	6	×	÷
1	2	3	+	-
0	.	=

Радиальное (нормальное) ускорение

Вычислить, найти радиальное (нормальное) ускорение по формуле (5) через линейную скорость

Вычислить, найти радиальное (нормальное) ускорение по формуле (5) через угловую скорость

Радиальное (нормальное) ускорение

См. также

Разделы

Калькулятор

Дополнительно